4.9 PROBLEMAS DE OPTIMIZACIÓN

 PROBLEMAS DE OPTIMIZACIÓN

La optimización es una rama del cálculo que se ocupa precisamente de esto: encontrar los valores óptimos de una función que maximizan o minimizan una cantidad deseada, como la ganancia, el costo o la eficiencia.

Por ejemplo:

• El ranchero quiere escoger la mezcla de pastos para poder obtener el mayor aprovechamiento.

• Un científico desea escoger y aplicar la menor dosis de una vacuna para obtener el mayor aprovechamiento.
• Un fabricante desea minimizar el costo de producción de un producto.

 

Algunas veces, problemas que se presentan ante la vida real, pueden formularse y resolverse, al involucrar una función y así es como el cálculo se vuelve una herramienta muy poderosa para poder resolver este tipo de cuestionamientos.

EJEMPLO:

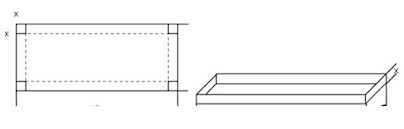
En una hoja tamaño carta realizará trazos de cuadrados que midan de lado 1, 2, 3, 5, 6,7, en cada una de las esquinas, después de trazar los cuadros, recortar de manera que quede unas pestañas a lo largo y ancho de la hoja y la pestaña se doblará para formar cinco cajas sin tapa como se muestra en la figura.

Ya que tienen elaboradas cada una de las cajas, el siguiente paso será calcular el volumen de cada una de ellas. Las operaciones las pueden desarrollar en la siguiente tabla, la sugerencia es que, si alguien trae en su celular el Excel, puede realizar las operaciones.

Después de llenar la tabla, debemos de hacer los siguientes cuestionamientos: 

a) Si con la hoja tamaño carta, me piden hacer una caja, donde contenga el mayor volumen, qué 

dimensiones son las que nos servirían. 

b) Podrá existir otras dimensiones que nos den un mayor volumen. 

c) ¿Qué pasa al momento de ir cambiando el valor del lado del cuadrado? 

d) ¿Cuál es el máximo valor que le podemos dar al cuadrado?

Para terminar la actividad, graficar los valores, en las abscisas (x) serán los valores del lado del cuadrado y las ordenadas (y), serán los valores del volumen. Decir que función representan los puntos.

Existen infinidad de problemas de aplicación, que se pueden resolver con la ayuda de los 

máximos y mínimos y para ello es importante seguir los pasos siguientes: 

a) Se hace un bosquejo del problema planteado y así poder interpretarlo 

b) Se escribe la función para obtener el máximo o mínimo según sea el caso. 

c) Se expresa la función en términos de una sola variable. 

d) Se encuentra la derivada de dicha función y se iguala a cero, para determinar los valores 

críticos. 

e) Se obtiene la segunda derivada y sustituimos los puntos críticos para aplicar el teorema. 

                            Si f’(c)=0 y f”(c)>0, entonces la función 

                             tiene un mínimo.  

                            Si f’(c)=0 y f”(c)<0, entonces la función  

                                                         tiene un máximo. 

Ahora resolveremos el problema planteado, que con una hoja tamaño carta, encontrar las 

dimensiones para poder construir una caja que contenga el mayor volumen. 

Siguiendo los pasos anteriores.

1.Hacemos el croquis para plantear el problema

2. Escribimos la función V=largo*ancho*altura 3. Expresar la función en términos de una sola variable, debes recordar que la variable en este caso será la altura (x)

V=(27.8-2x)(21.5-2x)(x)  realizando operaciones  

V=4x3-98.6x2+597.7x 

4. Obtenemos la derivada, igualamos a cero y obtenemos los puntos críticos 

V’=12x2-197.2x+597.7 

Igualando a cero y resolviendo la ecuación cuadrática por medio de la fórmula general. 

Obtenemos los valores de  x1=12.41

      y     

x2=4.009 

5. Los valores obtenidos (puntos críticos) se sustituyen en la segunda derivada 

V”=24x-197        para x=12.41    

   V”=100;     

x=4.009      

  V”=-100.784 

Y aplicando el teorema de la segunda derivada podemos deducir que cuando x=4.009, 

obtendremos una caja con el mayor volumen. 

Entonces las dimensiones de la caja:   altura 4.009,   largo= 19.782 y ancho=13.482 

Con este simple ejemplo te puedes dar cuenta de la importancia de tener el conocimiento del 

cálculo.